When I was learning how to tackle pwn challenges in CTFs, I had a tough time finding a single, clear guide that could show me the ropes of actually carrying out these exploits. That's why I decided to put together a complete guide that covers everything you need to know.
Having some background knowledge in C, stack, and assembly will be super helpful, and eventually a must, as we tackle more advanced topics. I will be using Kali Linux as the main platform for this series, but most of what we'll learn can also be applied to Windows.
What is Typecasting?
Typecasting takes place when the compiler converts a value into a different data type. Such conversions can often be mishandled and may result in unexpected behaviour that you can abuse to control the program's control flow. In this article, our focus will primarily be on C, which offers the most attack vectors to explore.
Explicit Type Casting
Explicit type casting is when the programmer explicitly specifies the desired type conversion. For example:
double x = 10.5;
int y = (int)x;
printf("%d\n", y);
Here, x is a double, and it has been specifically changed into an int using (int)x. This explicit casting clearly tells the system to convert the double value into an int.
Implicit Type Casting
When doing arithmetic operations, the compiler can automatically change the types of data to be compatible with each other. This occurs automatically by the language's rules and type system. For example:
int x = 10;
double y = 5.2;
double result = x + y;
printf("%lf\n", result);
The integer x is implicitly promoted to a double so that the addition operation can be performed without data loss. But how does it know what operand to change?
Overview of the Data Types
Here's a quick overview of various data types, their sizes in bytes, and their respective value ranges:
| Data Type | Size (bytes) | Range |
| short int | 2 | -32,768 to 32,767 |
| unsigned short int | 2 | 0 to 65,535 |
| unsigned int | 4 | 0 to 4,294,967,295 |
| int | 4 | -2,147,483,648 to 2,147,483,647 |
| long int | 4 | -2,147,483,648 to 2,147,483,647 |
| unsigned long int | 4 | 0 to 4,294,967,295 |
| long long int | 8 | -(2^63) to (2^63)-1 |
| unsigned long long int | 8 | 0 to 18,446,744,073,709,551,615 |
| signed char | 1 | -128 to 127 |
| unsigned char | 1 | 0 to 255 |
| float | 4 | 1.2E-38 to 3.4E+38 |
| double | 8 | 1.7E-308 to 1.7E+308 |
| long double | 16 | 3.4E-4932 to 1.1E+4932 |
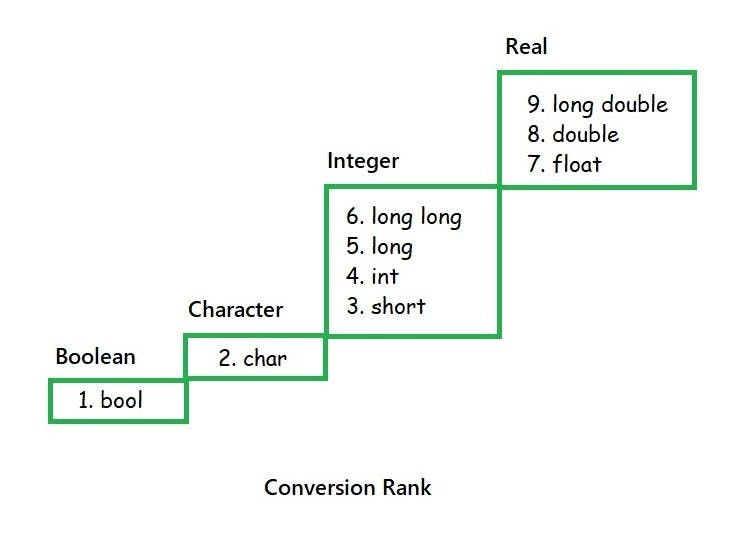
Generic Arithmetic Conversions
The intricate specifics of how arithmetic conversions determine what to convert fall beyond the scope of this article. You won't need an understanding for this article. It is a very large topic, and some more detailed information can be found here. But In a nutshell, it adheres to a data type hierarchy and a set of straightforward rules. When the values are of the same type, the conversion process concludes.
Floating Points Take Precedence: If any operand is a floating-point number, convert all operands to the floating-point type with the highest precision. No further conversion is needed.
Apply Integer Promotions: When both operands are of integer types, integer promotions are carried out on both operands. This entails converting any integer type narrower than an int into an int, while leaving unchanged any type that matches the width of an int, is larger than an int, or is not an integer type.
Conversion Based on Integer Conversion Rank: If the operands have the same sign (both signed or both unsigned), convert the operand with the lower integer conversion rank to the type of the operand with the higher integer conversion rank. This step finishes the conversion.
If the unsigned operand has a higher or equal integer conversion rank compared to the signed operand, convert the signed operand to the type of the unsigned operand.
If the signed operand has a higher integer conversion rank than the unsigned operand and a value-preserving conversion is possible, convert the unsigned operand to the type of the signed operand, completing the conversion.
If the signed operand has a higher integer conversion rank than the unsigned operand, but a value-preserving conversion is not possible, convert both operands to the unsigned type corresponding to the type of the signed operand. This is the final step in the conversion process.
If you don't know what a "signed" data type is, it will be further discussed below. But how does the compiler convert between different signs, sizes and ranges?
Conversion Type:
Although typecasting works most of the time, it's not perfect. To help learn how C deals with conversion. I wrote a program here%20TypeCasting) that will allow you to simply convert to and from different data types.
From:
[0] signed char
[1] unsigned char
[2] short int (or short)
[3] unsigned short int (or unsigned short)
[4] int
[5] unsigned int
[6] long int (or long)
[7] unsigned long int (or unsigned long)
[8] long long int (or long long)
[9] unsigned long long int (or unsigned long long)
[10] float
[11] double
[12] long double
Enter the first corresponding type index: 3
Enter the second corresponding type index: 2
Enter original Value: 65535
Original Unsigned Short Int Value: 65535
Converted to Short Int Value: -1
There are 3 different types of typecasting:
Narrowing
This occurs when a value is converted to a data type with a smaller range. For example, converting an int to an short int is a narrowing conversion. It may result in data loss if the int value is larger than the size of the value that the short int can hold.
Here is an example in C:
Enter the first corresponding type: int
Enter the second corresponding type: short int
Enter original Value: 1011135
Original int Value: 1011135
Converted to short int Value: 28095
Breaking this down into binary:
Original Int (4 bytes): 010101010101111|0110110110111111
Short Int (2 Bytes): |0110110110111111
As you can see, the operation simply disregards the larger bits.
Signed Conversion:
This occurs when a data type's sign convention is changed. For example, converting a negative int to an unsigned int will be converted incorrectly. But to understand how sign conversion works, let's first understand how the sign convention works.
Two's Complement representation
To understand signed conversion, let's begin by getting a handle on how a signed data type operates. C relies on what's known as Two's Complement representation. In this case, we'll illustrate it using just 4 bits, and it essentially boils down to two key aspects:
The leftmost bit, also known as the most significant bit (MSB), serves as the sign bit. It tells us whether the number is positive (0) or negative (1).
The rest of the bits follow the standard binary rules to represent the magnitude of the number.
Let's provide examples for both positive and negative numbers:
Example 1: Positive Number
Suppose we need to convert 6 into a 4-bit binary representation. 6 can be represented as (1 × 2²) + (1 × 2¹) + (0 × 2⁰) = (6)₁ or 110. As it is not negative, the MSB is 0 thus the 4-bit signed binary representation of 6 is 0110.
Example 2: Negative Number
Now, let's consider the value -6. We can start by converting 6 into binary, which gives us 0110. Next, we invert all the bits, resulting in 1001. Finally, we add 1 to this inverted value, yielding 1010. So, the final representation of -6 in Two's Complement is 1010.
Base 10: -6
-----------------
6 in binary: 0110
Inverted: 1001
Add 1: 1010
-----------------
Final represntation: 1010
How Sign Conversion Works
How can we weaponize this in C? When performing sign conversions in C, it involves a direct translation with no bit swapping. As a result, the sign bit is also directly translated, potentially leading to an unexpected value.
Enter the first corresponding type index: unsigned short int
Enter the second corresponding type index: short int
Enter original Value: 65500
Original Unsigned Short Int Value: 65500
Converted to Short Int Value: -36
Let's look at the conversion in binary:
unsigned short int (2 bytes): 1111111111011100
short int (2 Bytes): 1111111111011100
The sign bit was directly translated to the short int, which is a signed data type. Which gives us a value of -36.
This process occurs when a value is converted to a data type with a larger range. When converting from a smaller type to a larger type and the original type is unsigned, it fills all extra bits with 0. If the original type is signed, it uses the sign's bit value and copies it into the extra bits of the new type.
NEGATIE CONVERSION
Enter the first corresponding type index: short int
Enter the second corresponding type index: int
Original Short Int Value: -5
Converted to Int Value: -5
POSTIVE CONVERSION
Enter the first corresponding type: unsigned short int
Enter the second corresponding type: unsigned int
Original Short Int Value: 5
Converted to Int Value: 5
There are no issues when widening the data type, provided the destination data type maintains the same sign convention (either signed or unsigned) as the source data type. Errors occur when there is a disparity in the sign representation between the source and destination data types.
Enter the first corresponding type index: short int
Enter the second corresponding type index: unsigned int
Enter original Value: -9
Original Short Int Value: -9
Converted to Unsigned Int Value: 4294967287
Now, here's a CTF challenge that applies these principles. I suggest trying to work out the solution before peeking below.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define USERNAME_LEN 6
#define NUM_USERS 8
char logins[NUM_USERS][USERNAME_LEN] = { "user0", "user1", "user2", "user3", "user4", "user5", "user6", "admin" };
void init() {
setvbuf(stdout, 0, 2, 0);
setvbuf(stdin, 0, 2, 0);
}
int read_int_lower_than(int bound) {
int x;
scanf("%d", &x);
if(x >= bound) {
puts("Invalid input!");
exit(1);
}
return x;
}
int main() {
init();
printf("Select user to log in as: ");
unsigned short idx = read_int_lower_than(NUM_USERS - 1);
printf("Logging in as %s\n", logins[idx]);
if(strncmp(logins[idx], "admin", 5) == 0) {
puts("Welcome admin.");
system("/bin/sh");
} else {
system("/bin/date");
}
}
The core program flow can be summarised as follows:
The program begins by defining an array of usernames (logins) and initialising it with 8 usernames, one of which is "admin."
It then prompts the user to input an index corresponding to the user they wish to access.
The program utilises the "read_int_lower_than()" function, which performs the following steps:
a) Reads an integer input from the user.
b) Checks if the input is greater than 7. If it is, an error message is displayed, and the program exits.
c) It will return the index number.
If the selected index is "admin," the program spawns a shell.
Additionally, in the provided code, the "read_int_lower_than()" function returns an integer, which is then assigned to the variable "idx," with the type of an unsigned short int.
If we can somehow supply a number that will pass an int through the condition "less than 7" and when converted from an int to an unsigned short int gives us 7, we will be able to get the shell.
To achieve an unsigned integer value of 7 from a converted integer, we know:
The first 16 bits of data are discarded during the conversion. This includes the MSB.
The int value must be less than 7.
The last 4 bits should equal 0111.
Since an int is signed, we can make it negative, fulfilling the condition that the int value must be less than 7. Now we need to construct a number that equals 7 when converted from an int to an unsigned short int. Let's make it in binary:
1000 0000 0000 0000 0000 0000 0000 0111
In this case, the second to the 16th bits can be junk, while the last 4 bits equal 0111. This results in the integer number of -2147483641, which fulfils both conditions.
.\a
Select user to log in as: -2147483641
Logging in as admin
Welcome admin.
More Examples:
This website here is full of in-depth examples.
Conclusion
Thanks for reading this article. If you have any questions you can dm me. I will aim to try and get a new article out every 1-2 weeks, with the next article about buffer overflows.
Credits:
C Language Issues
C Language Issues for Application Security
