The Diffie-Hellman key exchange is a private-public key (asymmetrical) encryption used to establish a shared secret key. When using a symmetrical encryption, such as DES, you face a major problem. How do you share the key without leaking it to unwanted parties? You would have to send it threw a secure line but can any line truly be secure? This is when the Diffie-Hellman key exchange solves this problem. It allows two parties to securely establish a key on an insecure line of communication.
The Diffie-Hellman key exchange was created in the 70s by Whitfield Diffie and Martin e. Hellman in this landmark paper. It was the first known public-private key cryptography known to the public. RSA was created before the Diffie-Hellman key exchange between 1969 and 1973 by James Ellis, Clifford Cox and Malcolm Williamson but it was classified by Government Communication Headquarters (GCHQ), a UK intelligence agency. Now, the Diffie-Hellman key exchange is so successful it was even used to connect to this website.
How does the Diffie-Hellman key exchange work?
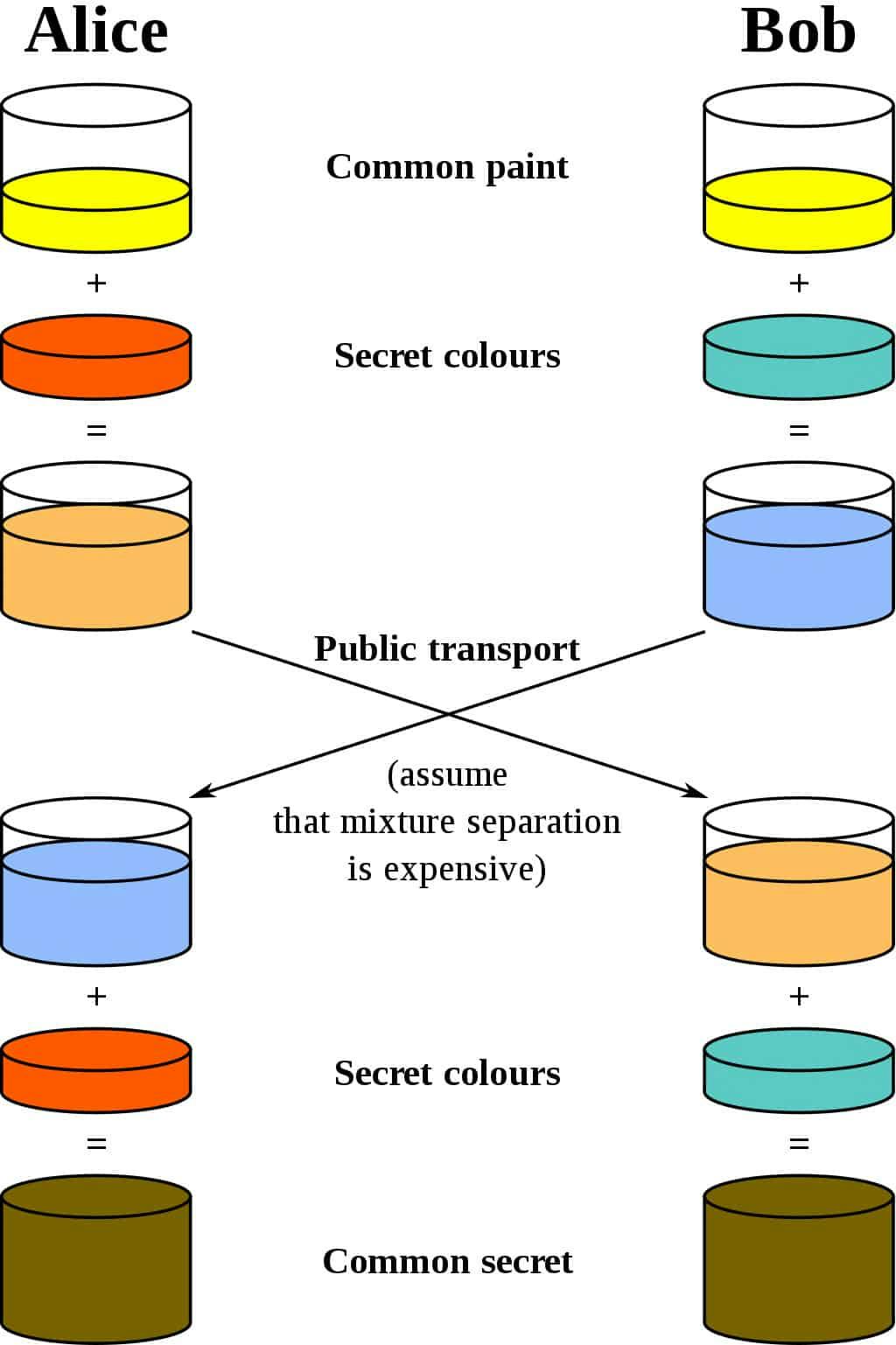
The Diffie-Hellman key exchange uses a lot of math, so let's start by using colour.
 Credit: What is the Diffie–Hellman key exchange and how does it work?, Josh Lake
Credit: What is the Diffie–Hellman key exchange and how does it work?, Josh Lake
Alice and Bob both decide on a predetermined common paint. In this case, it is yellow. They each choose an additional secret colour that they don't show anyone else. Alice chooses red and Bob chooses green.
Now they mix the predetermined common paint and their secret colour. in this case, the predetermined common paint colour is yellow. Alice will mix yellow and red which will produce a light orange. Bob will mix yellow and green which will produce a light blue.
Bob and Alice now share their mixed colours to each other. Alice will share her colour of light orange to Bob. Bob will share his mixed colour of light blue to Alice.
Finally, you mix the other person's shared colour and your own secret colour. Both Alice and Bob will have the remaining colour brown. The important part of this exchange is that the colour brown is only known to Alice and Bob. In the Diffie–Hellman key exchange the colour brown would be your secret key. You could use this key for algorithms such as DES or AES. Before looking into the mathematical concept, you need a clear understanding of the above concept.
How Diffie-Hellman key exchange works mathematically.
I will be explaining the most basic mathematical version of the key exchange in this section.
Before getting started with the Diffie-Hellman key exchange. We must first publicly decide on two numbers that will be publicly known. We need a prime (p) number and a base (g). The base (g) can be any number smaller than the p. In this case p = 14 and g = 6.
Now, Alice and Bob have to decide on a secret individual number that only they will know. In this case, Alice will choose 6 while Bob will choose 4.
a=6
b=4
We then must put these numbers threw a one-way function. This means that it is easy to calculate but incredibly hard to reverse. One way functions use modulus arithmetic. If you do not know what modulus arithmetic is Computer Hope has a good explanation but essentially it is the remainder division we did as kids. Modulus just takes the remainder, so 11 mod 4 = 3.
Alice will get A by using this one way functionA = g<sup>a</sup> mod p .
A = g<sup>a</sup> mod p
A = 6<sup>5</sup> mod 14
A = 7776 mod 14
A = 5
Bob will get B by using this one way function B = g<sup>b</sup> mod p.
B = g<sup>b</sup> mod p
B = 7<sup>4</sup> mod 14
B = 2401 mod 14
B = 6
Alice will now send her number A to Bob and Bob will send his number B to Alice. A and B will be publicly known. Now both parties will be able to calculate their shared secret.
Alice will calculate the secret by using the formula s = B<sup>a</sup> mod p.
s = A<sup>b</sup> mod p
s = 5<sup>7</sup> mod 14
s = 78,125 mod 17
s = 5
Bob will similarly calculate the secret. He will use s = A<sup>b</sup> mod p.
s = B<sup>a</sup> mod p|
s = 6<sup>5</sup> mod 14|
s = 7776 mod 17|
s = 5
Now they both have the shared secret of s = 5. Any would-be attacker that intercepted the shared would struggle to figure out s using the available information of A, B, g and p.
Below is a table that outlines the whole process.
| Alice | Shared | Bob |
| a=5 | p=14, g=6 | b=7 |
| A = ga mod p | B = gb mod p | |
| A = 65 mod 14 | B = 74 mod 14 | |
| A = 7776 mod 14 | B = 2401 mod 14 | |
| A = 5 | B = 6 | |
| A=5, B=6 | ||
| s = Ba mod p | s = Ab mod p | |
| s = 65 mod 14 | s = 57 mod 14 | |
| s = 7776 mod 17 | s = 78,125 mod 17 | |
| s = 5 | s = 5 |
This is a very weak version of the Diffie-Hellman key exchange as we are using a very small number. Prime (p) should at the very least be 2048 bits long. It also suffers from a lack of authentication, meaning anyone could be Bob.
Below is an example of a 2048-bit long number.
# a 2048-bit long number
1994641991657874238432584134916742769831626498728552748641213829416447744326318497317853615112452218299162248281941591219232629183284639871598555636789761746149615517811395589398861114178718851749455442924736594729825457397846951983358839924883789411234344
Ending Notes
If you are still interested and want to know more comparitech has a really good article.
I hope you enjoyed this article about the Diffie-Hellman exchange. If you have any questions you can always leave a comment below or feel free to reach out to me on Twitter at @dingo418.
Sources
What is the Diffie–Hellman key exchange and how does it work?


